มาหาค่าพายจากการสุ่มเลขกันเถอะ
ให้ฟังก์ชันนึงสมมติว่าชื่อ
rand()สามารถสุ่มเลขระหว่าง 0 ถึง 1 ได้ จงหาค่าพายจากฟังก์ชันนี้ โดยสามารถเรียกฟังก์ชันrand()ได้ไม่จำกัดครั้ง
กล่าวคือให้หาค่าพายจากการสุ่มเลขระหว่าง 0 ถึง 1
โจทย์นี้1 ได้มาจาก YouTube ช่อง Joma Tech ดูเป็นโจทย์ที่ไร้สาระมากเลยใช่มั้ย แบบจะไปทำได้ไง แต่ถ้าเห็นเฉลยแล้วเชื่อว่าทุกคนจะอ๋อแน่นอน เฉลยของโจทย์นี้บอกได้ว่าสวยมาก อยากให้ทุกคนลองคิดดูก่อน แล้วค่อยไปดูเฉลยด้านล่างนะ😋
เฉลยจ้า
หลักการคือเราต้องมองโจทย์ให้เป็นระนาบ 2 มิติ โดยที่แต่ละแกนจะยาวตั้งแต่ 0 ถึง 1 แบบนี้
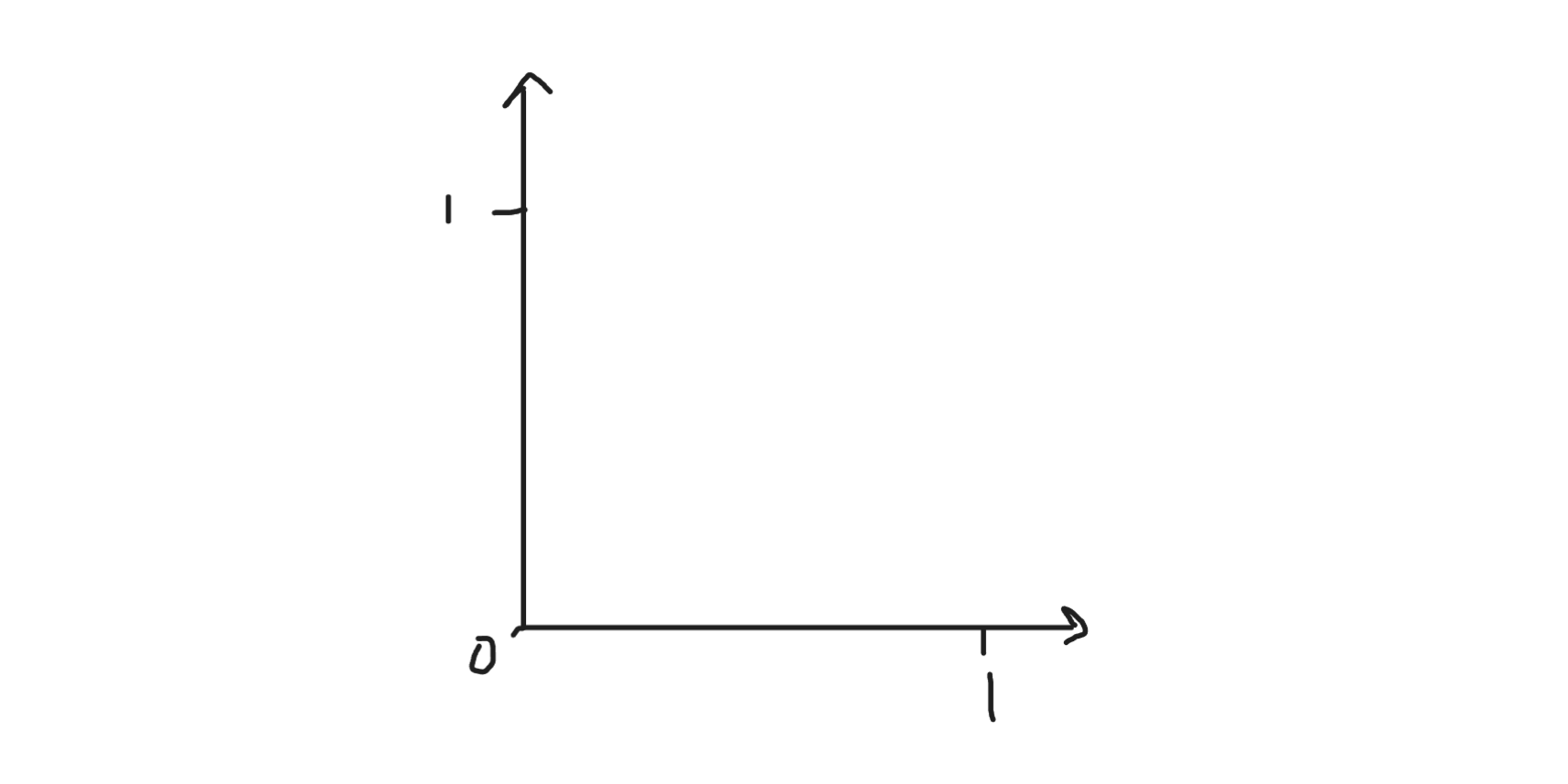
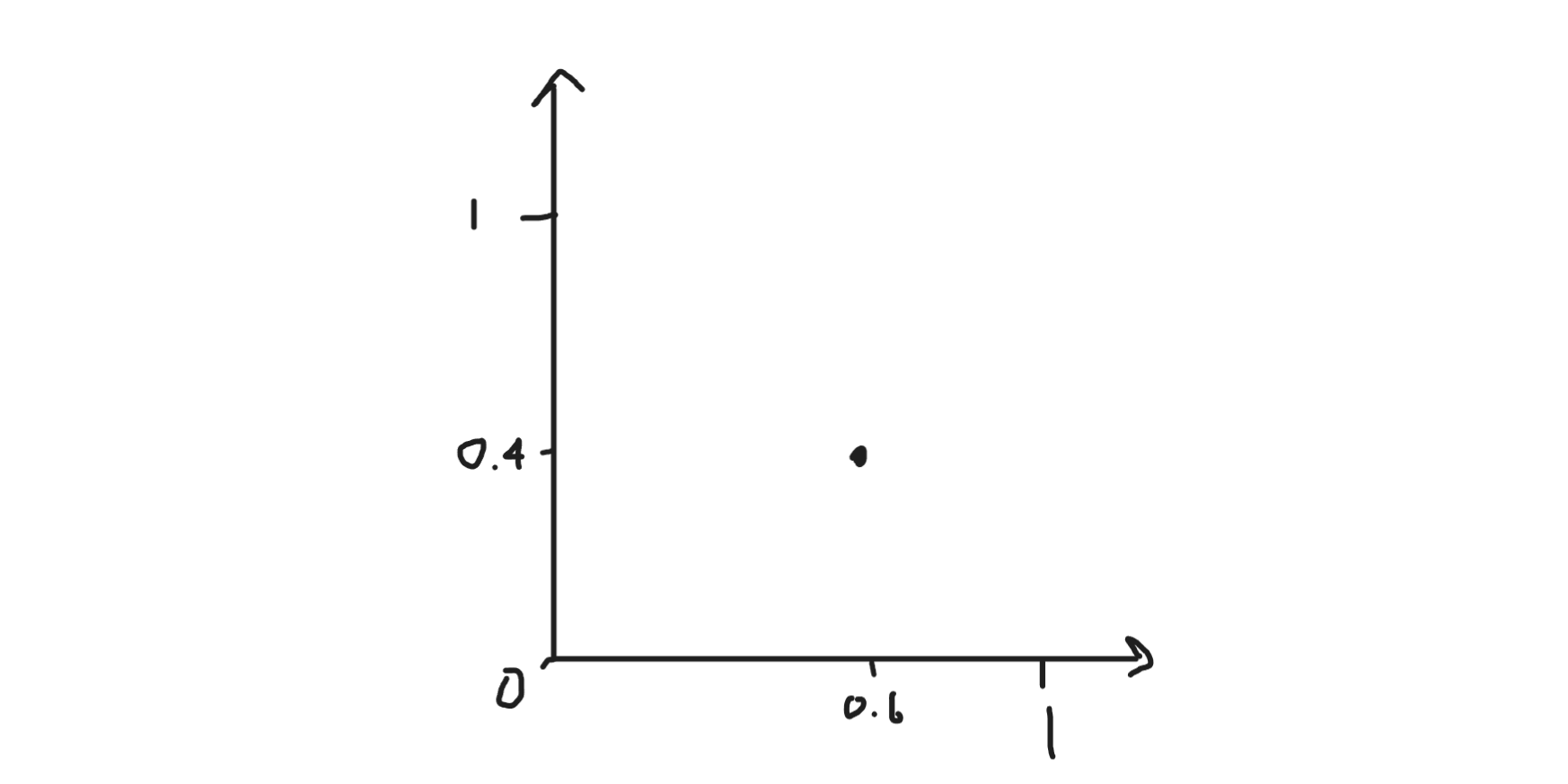
เราจะทำการสุ่มจุดบนระนาบนี้ด้วยวิธีการสุ่มค่า x และ y ทีละค่า แล้วเราจะได้จุดจุดหนึ่งขึ้นมา เช่นถ้าเราสุ่มค่า x ได้ 0.6 และ y ได้ 0.4 ก็จะเป็นจุด $(0.6, 0.4)$ ขึ้นมา
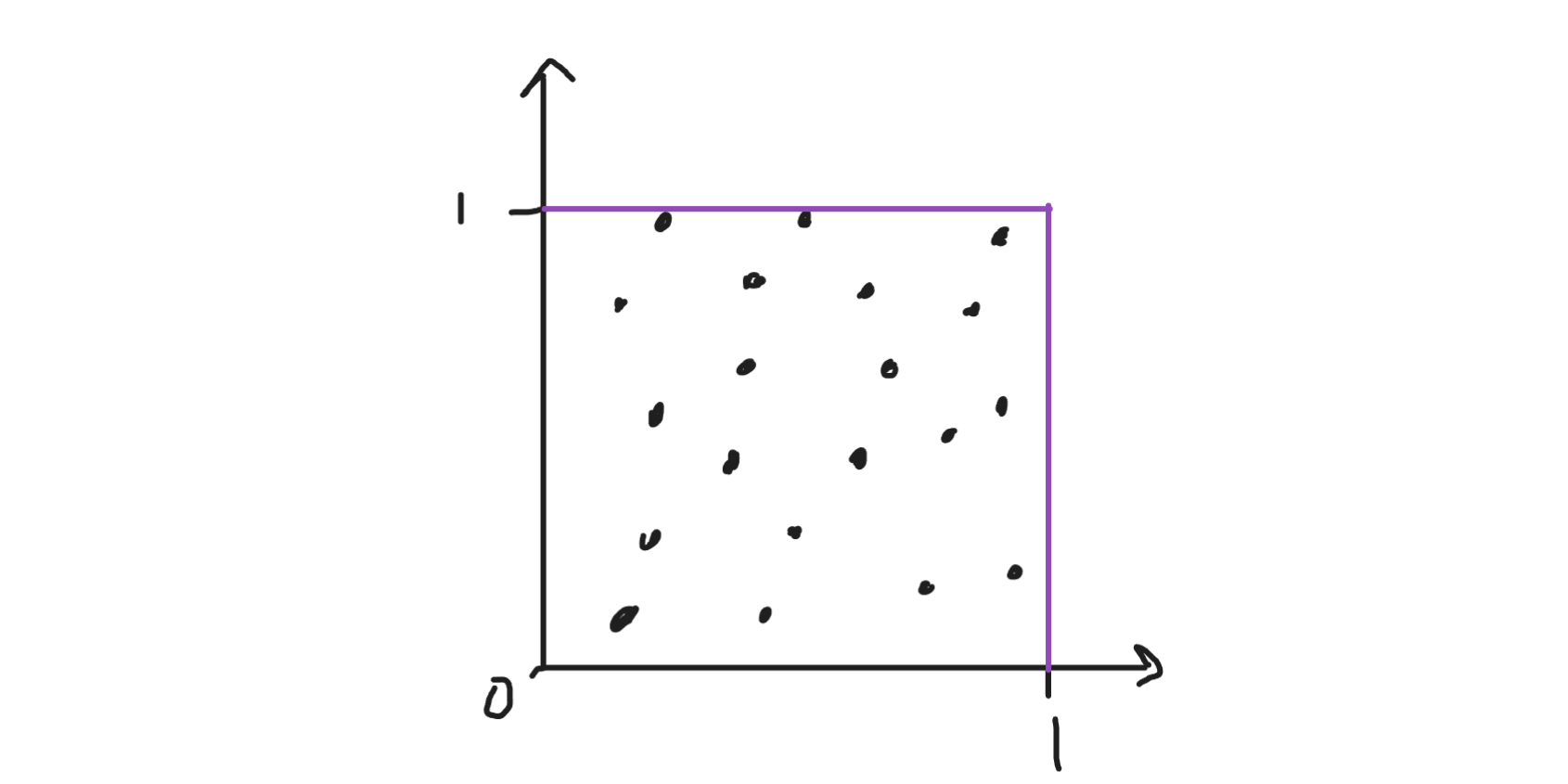
ทีนี้สมมติว่าเราสุ่มลงไปให้ได้ซักประมาณ 20 จุด และตีกรอบสี่เหลี่ยมขนาด 1x1 ครอบไว้ด้วย
และแน่นอนว่าถ้าเราพูดถึงค่า $\pi$ ก็ต้องมีวงกลมเข้ามาเกี่ยวข้อง ดังนั้นเราจะเอาวงกลมขนาดรัศมี 1 มาวาดด้วย
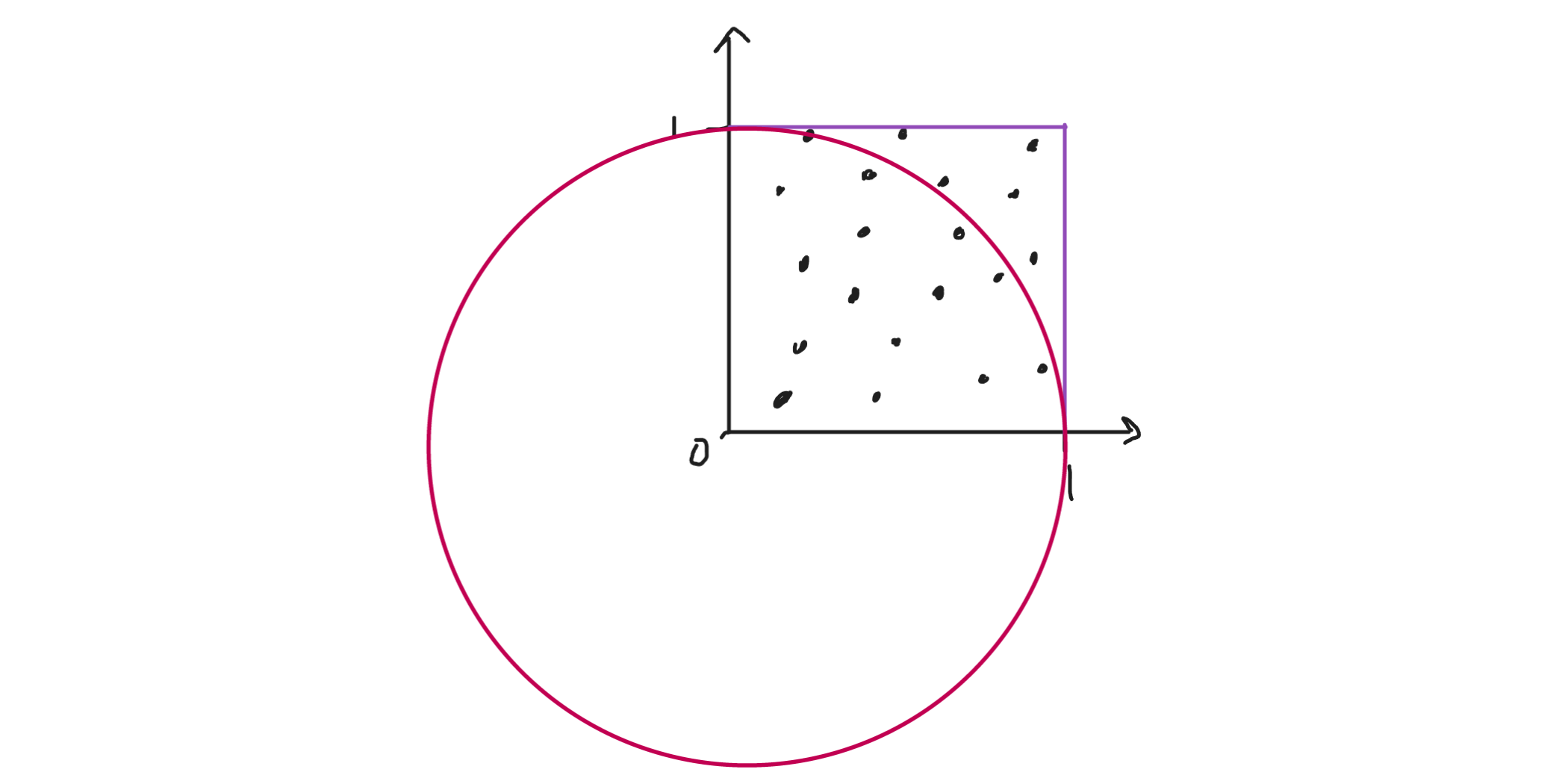
จะเห็นได้ว่าในสี่เหลี่ยม 1x1 นี้ มีทั้งจุดที่อยู่ในเสี้ยววงกลม และจุดที่อยู่นอกวงกลม ลองจินตนาการว่าถ้าเราสุ่มจุดเพิ่มลงไปบนระนาบเรื่อย ๆ จนมากพอ จะสังเกตได้ว่า
\[\frac{N_c}{N_s} \approx \frac{A_c}{A_s}\]โดยให้
- $N_c$ คือ จำนวนจุดที่อยู่ในเสี้ยววงกลม
- $N_s$ คือ จำนวนจุดทั้งหมดในสี่เหลี่ยม
- $A_c$ คือ พื้นที่ของเสี้ยววงกลม
- $A_s$ คือ พื้นที่ของสี่เหลี่ยม
ดังรูป
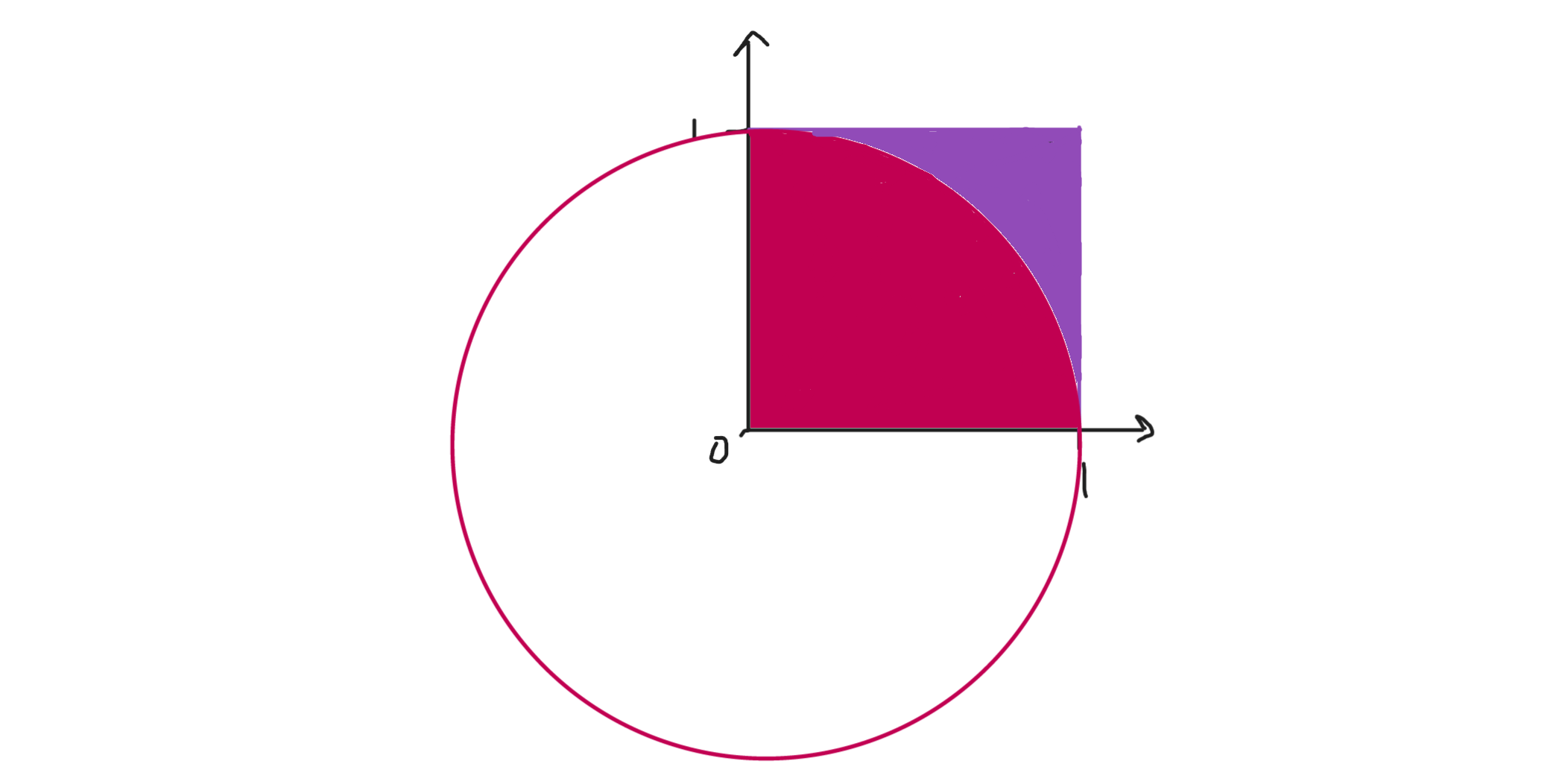
ซึ่งพื้นที่สี่เหลี่ยมในที่นี้คือ $1 \times 1 = 1$ ตร.หน่วย และพื้นที่เสี้ยววงกลมคือ $\frac{\pi(1)^2}{4} = \frac{\pi}{4} $ ตร.หน่วย ดังนั้นจะได้ว่า
\[\begin{align} \frac{N_c}{N_s} &\approx \frac{A_c}{A_s} \\ \frac{N_c}{N_s} &\approx \frac{\frac{\pi}{4}}{1} \\ \pi &\approx 4 \times \frac{N_c}{N_s} \end{align}\]ฉะนั้นถ้าเราสามารถหาจำนวนจุดที่อยู่ภายในเสี้ยววงกลม และจำนวนจุดที่อยู่ในสี่เหลี่ยมได้ เราก็จะสามารถหาค่า $\pi$ ได้
แล้วเราจะรู้ได้ยังไงล่ะว่าจุดนั้นอยู่ในพื้นที่วงกลมรึเปล่า ง่ายมาก! แค่หาระยะทางหว่างจุดใด ๆ ถึงจุดศูนย์กลาง $(0, 0)$ ถ้าระยะห่างนั้นน้อยกว่าหรือเท่ากับรัศมี (1 หน่วย) ก็แปลว่าจุดนั้นอยู่ในวงกลม ซึ่งสมการระยะห่างจุดสองจุด $(x_1, y_1)$ และ $(x_2, y_2)$ คือ
\[d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\]และเราสามารถแทนค่า $x_2, y_2$ ด้วย $(0, 0)$ ได้เลย ดังนั้นสมการระยะห่างจะกลายเป็น
\[d = \sqrt{x^2 + y^2}\]ดังนั้นเราก็สามารถเขียนโปรแกรมเพื่อหาค่า $\pi$ ได้ดังนี้
import random
def rand():
return random.uniform(0, 1)
def is_in_circle(x, y):
return x**2 + y**2 <= 1 # ใช้ 1 ได้เลยเพราะรากที่สองของ 1 ก็คือ 1
# n คือจำนวนจุดทั้งหมดที่เราจะสุ่มลงไป
def estimate_pi(n):
num_in_circle = 0
for _ in range(n):
x = rand()
y = rand()
if is_in_circle(x, y):
num_in_circle += 1
return 4 * num_in_circle / n

author